이지원의 공부기록

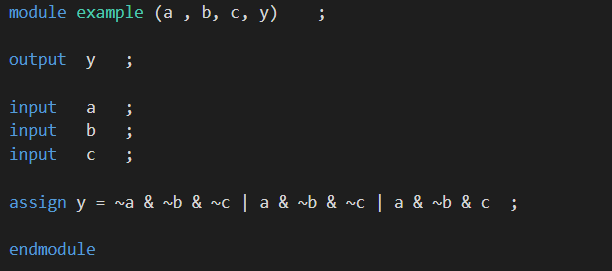
지난 포스팅에 애더까지 만들고

testbench를 이용하여 시뮬레이션도 돌려보았다.

​

오늘은 MUX (먹스) 를 만들어보겠다.

​

먹스 (MUX) 란 Multiplexer로

출력에 연결하는 N개의 입력 중 하나를 선택하는것이다.

​

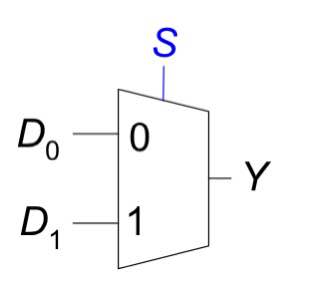
예를 들면 위와 같은 구조에서

S가 0이라면 D0의 값이 Y가 되고

S가 1이라면 D1의 값이 Y가 되는것이다.

​

​

그렇다면 이제 verilog를 이용하여 이러한 mux를 어떻게 디자인하냐,,,!

​

먼저 2:1 mux를 생각해보자

2:1 mux라면 선택지가 d0와 d1 이렇게 두가지만 있는

위의 예시에서 보여준 형태이다.

​

module 이름을 써주고 입출력을 써준 후

assign으로 할당하여준다.

assign 문에서 ?의 역할이

s에 따라 d1과 d0중 선택하겠다는 뜻이다.

​

따라서 mux에서는 이렇게 써준다.

여기서 주의할건 뒤에가 0일때라는거임!

그래서 0일 때 d0를 택할거니까 d1:d0로 써줌

​

그렇다면 이번에도 마찬가지로 내가 짠 이 mux가 제대로 작동하는지를 확인하기 위해

testbench를 간단히 짜서 확인해보자

​

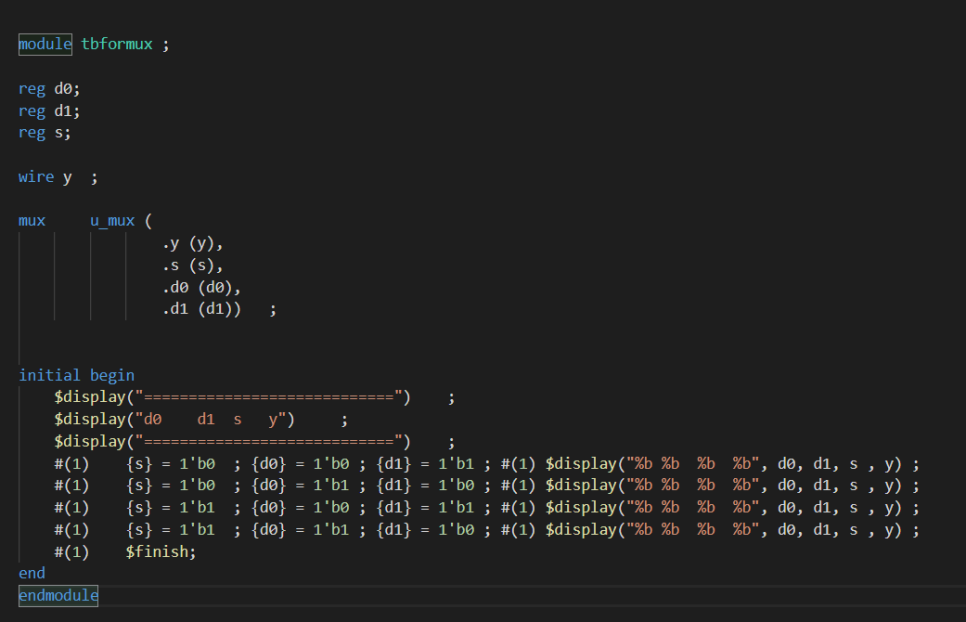
간단히 module 이름은 tbformux로 하고

​

입력은 reg 출력은 wire 선언을 해준다.

​

그리고 우리가 확인해볼 mux를 써서 불러와주고

각각의 입출력 옆에 들어갈 값들을 써준다.

​

그리고 display를 이용하여 화면에 나타나는걸 적어준다.

s가 0과 1에 따라 달라지므로 0을 넣었을때와 1을 넣었을때를 보여주기 위해

0과 1을 넣어주고

​

그에 따라 d0와 d1이 나오는걸 보여주기 위해

d0와 d1에도 다른 입력값을 넣어준다.

​

그리고 시뮬을 돌려보면

​

s의 값이

0일때는 d0 의 값이 y로 나오고

1일때는 d1의 값이 y로 나오는 것을 확인할 수 있다.

​

지난 포스팅에는 1-bit adder를 연결하여

4-bit adder를 만들었다.

​

이번 포스팅은 그렇게 만든 adder를 실험할 수 있는 testbench를 짜 볼 것이다.

​

우선 testbench 란 우리가 만든 dut (device under test) 를 말 그대로 test 할 수 있게 해주는 것이다.

​

앞에서 만든 adder는 dut이다. 이 dut만 가지고서는 제대로 작동하는지 알 수 없기 때문에

testbench를 이용하여 시험해주는 것이다.

​

예를 들어 함수 f(x)를 만들었다면 그 함수 f(x)의 x에 어떤 값을 넣었을 때

우리가 생각한 값이 나와야지 함수 f(x)가 제대로 작동하는지 알 것이다.

​

그런 x에 값을 넣는 동작을 testbench로 해주는 것이다.

​

testbench 또한 우리가 만든 dut를 test 하는 것이므로

시험하려는 dut와 입출력이 똑같아야 한다.

​

(다르면 오류 뜨므로 주.의. 오류 뜨면 짜증남)

​

* dut에서는 입력을 input , 출력을 output으로 적었지만

testbench를 작성할 때는 입력은 reg로 선언하여 적고 출력은 wire로 적어준다.

​

그리고 각 모듈의 이름을 써주고 입출력 옆에 ( ) 에 각각 넣을 입력을 적어준다.

​

예시로 저번 포스팅에서 만든 adder에 관해 testbench를 작성하면 다음과 같다.

​

항상 시작은 module로 시작한다.

그리고 dut와 다르게 입력은 reg 출력은 wire 선언 후 작성한 걸 볼 수 있다.

​

그리고 각각 입력을 random하게 넣어주면서 화면에 출력되는 output 값을 확인하면 adder가 제대로 작동하는지

확인할 수 있다.

​

이와 같이 작성한 testbench를 modelsim을 이용하여 돌려보면

​

​

이러한 웨이브 형태가 나온다.

우리는 이진수보다는 역시 10진수가 알아보기도 편하고 마음도 편하므로 ^^,,,

상큼하게 10진수로 바꿔준다

​

그리고 웨이브를 잘 살펴보면

a와 b 그리고 carry in이 랜덤하게 들어오는 것을 볼 수 있다.

​

그리고 그에 따라 sum인 출력값 s1을 보면 2+4+1=7

로 7이라는 값을 가지는것을 볼 수 있다.

또한 이는 다른 방법으로 작성한 두개의 4-bit adder에서

동일한 결과 값이 나오는걸 볼 수 있다.

(s1과 s2의 값이 같고, co1과 co2의 값이 같다.)

​

다음 웨이브를 보면 ci (carry in ) 값이 없고

a,b 값이 8과 1이므로

8+1+0 = 9

로 s1, s2의 값이 9인것을 볼 수 있다.

​

이를 display 창 (화면에 표시되게끔 작성했으므로)

을 통해 보면 다음과 같다.

​

각각 표에서 ci와 a,b 를 더한값이 s1, s2 인것을 확인할 수 있다.

​

이렇게 adder (덧셈기) 를 만들었다.

​

지난 포스트에 1-bit adder를 만들었으므로

오늘은 4-bit Adder를 만들어보도록 하겠다.

​

​

지난 시간에 만든 1-bit adder를 연결하면

4-bit 인 adder를 만들 수 있다.

​

구조를 살펴보면 다음과 같다.

1bit adder에서 나온 carry out이

다음 adder의 carry in 으로 들어가게 되고

이렇게 4번을 하면서 4-bit 짜리를 만들 수 있는것이다.

​

따라서 1-bit adder를 이용한다면 간단하게 만들 수 있다.

​

먼저 1-bit adder를 다음과 같이 적어주고

여기서 이 모듈의 이름이 fa 라는걸 주의깊게 보자

​

4-bit adder를 만들것이므로

각각의 입출력에 [3:0]을 작성해서 4bit로 만들어준것도 주의해야한다.

​

(* 작동하려고 쓰는것보다 비트수를 적게 할당하면 오류가 날 수 있다. 추후에 다시 설명하겠다)

​

​

그리고 맨 위 그림에서 보듯이 각각의 1-bit adder에서 나온 carry out과

그 다음 adder로 들어가는 carry in은 입출력이 아니므로 wire로 선언해서 적어줘야 한다.

​

그리고 1-bit adder의 모듈이름이 fa 였으므로

fa 라고 선언해준 후 이름을 적고 각각의 입출력 옆 ( ) 속

넣어줄 입출력들을 적어준다.

​

첫번째 adder에서 나오는 carry out이

다음 adder의 carry in 으로 들어가고

마지막 carry out은 출력의 carry out 인것에 주의해야 한다.

​

​

쿼터스에서 compile을 돌리고 RTL을 확인해보자

​

생긴건 복잡하게 생겼지만

저 빨간선처럼 각각의 1-bit adder로 들어가면서 합계가 나오는 걸 알 수 있다.

​

​

​

​

​

(Adder에 관한 이론적인 설명은 논리회로 카테고리에 추후 추가하겠다)

Adder는 기본적으로 carry와 sum 이 out값으로 발생하게 된다.

그러므로 설계를 하기 전 1-bit Full Adder의 carry와 sum에 대해 truth table을 살펴보면 다음과 같다.

For sum 

S = A'B'Cin + A'BCin' + ABCin + AB'Cin'

으로 나타낼 수 있다.

For carry out

Cout = AB + BCin + ACin 

으로 나타낼 수 있다.

이를 가지고 Dataflow style 로 1-bit Full Adder를 설계하면 다음과 같이 쓸 수 있다.

assign  다음에 위에서 나타낸 sum 과 carryout을 게이트를 이용하여 나타낸 것을 볼 수 있다.

이를 case문을 활용해서도 1-bit Full Adder를 설계할 수 있다.

위와 마찬가지로 입출력은 동일하지만 이번에는 assign문이 아닌 case 문을 활용하여 나타낸 것을 볼 수 있다.

case 안에 넣어준 입력 차례대로 ci a b 가 각각의 비트일 때 co와 s 가 어떤 비트를 가지는지를 하나하나 케이스별로 쓴 것이다.

또한 이는 베릴로그의 concatenation 문법을 사용하여 다음과 같이도 설계할 수 있다.

이렇게 1-bit Full Adder를 design 할 때도 여러 방법을 사용할 수 있다.

하드웨어를 기술하는 언어인 베릴로그

1) 베릴로그는 두 유형의 모듈이 있다.

   - Behavioral :  모듈이 무엇을 하는지 설명

   - Structural  :  간단한 모듈로부터 어떻게 설계되는지

2) Behavioral 

   verilog 에서는 시작할때 module 을 적어주고 그 다음 모듈 이름 , 모듈의 입출력, 원하는 동작, endmodule 순으로 적어준다. 간단한 예시를 보면 다음과 같다.

이렇게 기본적인 모듈을 만들고 이러한 모듈을 이용하여 더 큰 모듈을 생성할수도 있다.

논리회로에서 배운 AND, OR , NOT 게이트들을 사용하여 다양한 동작을 하는 모듈을 생성할 수도 있다.

2) 주의해야할 점

1. 대소문자를 구분해야 한다. (Example과 example 은 다르다. )

2. 숫자로 시작하는 이름은 안된다!!

3. 공백은 무시하고 작동함

3) Strtuctural 

   위에서 말했듯이 기본적인 모듈을 이용하여 연결한다고 생각하면 된다.

and 게이트와 inverter 게이트를 합친 모듈을 만들어보면 다음과 같다.

합칠 모듈은 그 파일 안에 들어있어야 한다. 그 후 새로운 모듈을 선언 해주고 연결할 선이 있다면 wire 선언을 해주어야 한다. 그 후 모듈 이름을 적어 불러온 후 각각의 입출력 옆에 ( ) 속 입력들을 적어준다. 

위의 예시에서 and 게이트의 출력을 inverter 게이트의 입력으로 넣을것이므로 

wire 선언을 해준 것을 and 게이트의 출력으로 적어주고 inverter 게이트의 입력으로 넣어주었다.

*) module 옆에 적는 아이를 port list 라고 한다. 여기에 입출력을 다 적어주지 않아서 오류가 자주 뜨므로 꼭 적어줄 것!,

우리가 흔히 일상에서 쓰는 숫자들은 10진수이다.

이를 0과 1만 사용하여 2진수로도 나타낼 수 있고

0~8까지만 사용하여 8진수, 0~16까지만 사용하여 16진수로도 나타낼 수 있다.

1) 일의 자리부터 2^0 십의 자리는 2^1로 생각해서 더해주면 된다.

ex) 0 (2) = 0 , 10(2) = 2+0 = 2,  11(2) = 2+1 = 3,   101(2) = 4+0+1 = 5 

(2)는 이진수를 나타낸다.

이와 마찬가지로 16진수는 0~15까지를 사용하여 나타낸다. 이때 10부터는 A로 나타낸다.

ex) 4AF(16) = 16^2X4 + 16^1X10 +16^0X15 = 1199 

2) 그렇다면 이러한 2진수의 덧셈은 어떻게 할까?

10진수의 덧셈에서는 10을 넘기면 다음 자리에 1을 더해주었다. 이와 마찬가지로 2진수의 덧셈에서도 1과 1을 더할 때 다음 자리에 1을 더해준다.

EX) 10진수                                   EX) 2진수

3) 2진수로 부호를 나타낼 수 있을까?

정답은 나타낼 수 있다. 하지만 방법이 조금 다르다.

방법으로는 두가지가 있는데 첫 번째는 부호 및 크기의 2진수 표기법이다.

예를 들어 숫자 6을 2진수로 표현하면  110(2)이다.  ( 4+2+0 = 6 )

이때 앞에 한자리를 더해 +/- 를 나타낸다.

+6 : 0110

-6  : 1110

으로 나타낼 수 있다.

하지만 이렇게 나타내면 덧셈시 계산 결과의 오류가 날 수 있고, 0을 표시하려 할 때 1000과 0000의 두 가지 방법이 생기는 문제점이 있다.

그러므로 두번째 방법은 2의 보수를 사용하여 부호를 나타내는 것이다.

이 방법은 최상위 비트의 값이 2^(N-1) 대신 -2^(N-1)이라는 것을 제외하면 부호 없는 2진수와 똑같다.

먼저 구한 2진수를 반전시킨다음 1을 더하면 된다.

예를 들어 숫자 -2를 나타내려면

먼저 2(10) = 0010(2) 

이다. 그러므로 0010을 반전시키면 1101(2) 이 되고 여기에 1을 더해주면

  1110(2) 이 된다. 이것이 -2(10)을 이진수로 표현한 것이 된다.

여기서 주의해야 할 점은 덧셈을 할 때 N번째 비트에서 발생한 N+1 번째 비트는 버려야 한다!!